Path tracing relies on random sampling of light from the surrounding geometry, in order to approximate the global illumination. This task builds on the Ray Chopper task, but instead of just returning the color from the first hit, we now shoot another ray in a random direction from the hit. We combine the two colors (the one from the first hit, and the one from the second hit) to determine the color of the pixel. That is called path tracing with direct lighting. Of course, we could continue, and do another bounce, and then another. That would give a bit more accurate results, but because the effect of additional bounces is quite small, if we use direct lighting, then just a couple of bounces will be sufficient.

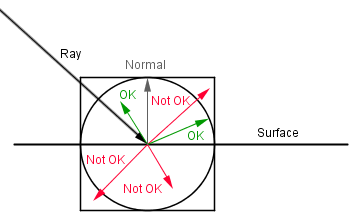
In order to generate a new random direction for the ray, one idea would be to generate a random vector from a cube. After this, you can test, if the generated vector is inside a sphere. If it is not, then generate a new vector. Otherwise the diagonal direction in the cube would get more random vectors (ie the distribution would not be uniform inside a sphere). Alternatively you can use another method from picking a random point directly from a sphere.

Next, you can check, if the vector is pointing to the same side of the surface, as the surface normal. If it is not, then just take the opposite vector.

Path tracing renders the scene a number of times, each time creating new random bounces. The results from all of those renders are averaged to get the final result. For this, two textures can be used. One stores the average from all the previous renders, and one will store the result of the current render. Each iteration, the textures can be switched.

In order to store this average value of a pixel, think about, what the average is. Usually it is written as:

$\bar{a}_n = \dfrac{a_0 + a_1 + ... + a_n}{n}$

We can assume, that we have that value stored in the first texture, but now want to add another value $a_{n+1}$ to it, and get the resulting average. If we want to get back to the sum, we would have to multiply the average with $n$. Our new average should be the average of $n+1$ values, so we also want to divide with $n+1$:

$\hat{a}_{n+1} = \bar{a} \cdot \dfrac{n}{n+1} = \dfrac{\bar{a} \cdot n}{n+1}$

This is almost what we want, but we are missing the value $a_{n+1}$. For that, we can just add to $\hat{a}_{n+1}$ the value $\dfrac{a_{n+1}}{n+1}$.

$\bar{a}_{n+1} = \bar{a} \cdot \dfrac{n}{n+1} + a_{n+1} \cdot \dfrac{1}{n+1}$

The coefficients we just found for updating the average, are $\dfrac{n}{n+1}$ and $\dfrac{1}{n+1}$. They always sum up to $1$, regardless on $n$, so it is a convex combination of the previous average and the new value. You can use the GLSL mix() function to calculate it.

In this task you should yse the base code from the Ray Chopper task and change it accordingly. Most of the code is exactly the same. The result should render a scene using path tracing with direct illumination described above (and also in the material). You should structure the scene in a way, where the effects of global illumination are apparent. Describe them with the submission.

Here are some important changes, that need to be done:

Application Side

• You need to use two textures to render onto. Two, because you can not render and read from a same texture. Flip them each iteration.
• You might also want to use two scenes. One will do the path tracing into the texture, another will just render one of the textures to see the result.
• Add uniforms for the time (to seed the random generator) and sampleWeight, that will be used to mix the current average with the new value.
• Change the scene accordingly. The chopper with rotating blades is not the best idea.
• You may need to also add a rotation functionality to the createCube function.

Fragment Shader

• Create methods to do the random reflection of an incident vector, given a surface normal. The idea was described above, and you might want to check out this site, to see, how to generate random numbers in GLSL.
• The method rayTrace would now be pathTrace, that would do one or two ray casts (0 or 1 bounce, you might want to use 0 for debugging). You can find the direct illumination exactly, like you did in the Ray Chopper task. For the indirect illumination, take into account the surface reflectance, you are bouncing from. For example, a completely red surface can not reflect green indirect illumination. For simplicity, use only the diffuse reflectance.

The results can look like this:

No bounces (only direct illumination)	Indirect illumination	Combined final result