The Bresenham's line idea can also be used to rasterize triangles. There are actually other shape rasterization algorithms that use the Bresenham's line idea (the Bresenham's circle for example).

The idea when rasterizing the triangle is that, we will first split the triangle in two pieces. The piece from the leftmost vertex to the middle vertex and the piece from the middle vertex to the rightmost vertex. Then we will use Bresenham's line algorithm to rasterize the two edges of the first piece. We need pairs of points on those edges that have the same x coordinate, then we rasterize the vertical line between them.

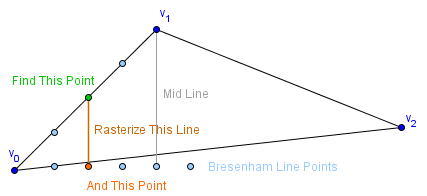
In other words, we will find all the vertical lines for each discrete x value from the vertex $v_0$ to $v_1$. This will fill the left piece of the triangle. Then we will consider the edge $[v_1, v_2]$ instead of $[v_0, v_1]$ and do the same with the right piece.

In order to find those points on the edges of the triangle, we need the Bresenham's line algorithm to give us a next y value for the next x. This means that using the algorithm from before that just draw that line in one go, will not work. We will, however, use the same idea as before (accumulating the slope as the error, increasing the other coordinate if the error becomes too big).

There is one more thing, just rasterizing a monochrome triangle is not all that fun. Usually there will be some attributes assigned to the vertices, like the color for example. We can interpolate those values along the triangle. Basically the color of each point inside the triangle can be represented as an convex combination of the colors of the vertices. The coefficients are called barycentric coordinates. If you assign colors for each vertex, then you need to consider first, how far along have you moved on the edges of the triangle, then where are you on the vertical line.

Here is a general picture describing it:

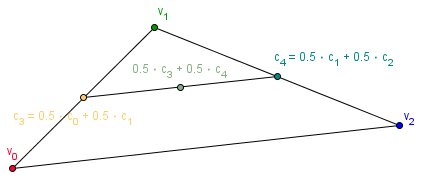
Task is to rasterize a triangle and interpolate the colors of the vertices smoothly over the raster.