The example in the material showed a Bezeri spline with $C^0$ smoothness. This is achieved by taking the last control point of the previous curve and using that as the first control point of the current curve. In other words, if we have curves with control points $p_0$, $p_1$, $p_2$, $p_3$ and $q_0$, $q_1$, $q_2$, $q_3$, then making sure that $p_3 = q_0$ will get us a continuous Bezier spline.

Examples of this can look like:

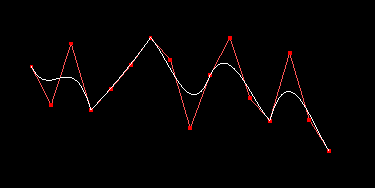
In this task we will create $C^1$ and $C^2$ smooth Bezier splines. Intuitively you can guess that a $C^1$ Bezier spline should have the points $p_2$ and $q_1$ symmetrically placed from $p_3 = q_0$. Mathematical explanation behind it is that if you take the derivative from the entire curve function, then you get that the derivatives in the knots (endpoints) equal:

$p'(1) = 3 \cdot (p_3 - p_2)$

$q'(0) = 3 \cdot (q_1 - q_0)$

You can read more about how to find this here: http://pomax.github.io/bezierinfo/#derivatives

Now, there are actually many ways how to achieve such a configuration for the control points. In this task we will be using the Stärk's construction. For the $C^1$ smoothness we take:

$p_3 = q_0 = 0.5 \cdot (p_2 + q_1)$

Visually this means that we place the joined point exactly between the neighbouring points.

Now, this also means that whatever value we gave it before, will get overwritten. So in reality we would only need two points for each curve that is not the first and the last curve. The endpoints of the curves that are surrounded by other curves, will get calculated. 

After this you should get $C^1$ smooth splines that may look like:

For $C^2$ smooth splines we can mathematically find out that:

$p''(1) = 6 \cdot p_3 - 12 \cdot p_2 + 6 \cdot p_1$

$q''(0) = 6 \cdot q_2 - 12 \cdot q_1 + 6 \cdot q_0$

In order for the second derivative to be equal in the knots between two curves $p$ and $q$, we can say that we need the following condition:

$p_3 - 2 \cdot p_2 + p_1 = q_2 - 2 \cdot q_1 + q_0$

Rearranging the terms we get:

$(p_3 - p_2) + (p_1 - p_2) = (q_2 - q_1) + (q_0 - q_1)$

We know that $(p_3 - p_2) = (q_1 - q_0)$, because this was the condition for the continuity of the first derivative, which we must have, if we want to talk about the continuity of the second derivative. Knowing this, we can now write:

$2 \cdot (p_3 - p_2) = 2 \cdot (q_1 - q_0) = (q_2 - q_1) + (p_2 - p_1)$

Visually this equation means that we need to have two similar triangles that share a tip:

Because the base $[p_1, q_2]$ of the larger triangle must be twice base $[p_2, q_1]$ of the smaller triangle, then the point $p_2$ must lie exactly in the middle of the line $[p_1, Tip]$ and similarly, the point $q_1$ must lie exactly in the middle of the line $[q_2, Tip]$. This means that if we fix the value for the $Tip$, then we have specified the values for $p_2$ and $q_1$. Because of that you might now notice, that we will need yet another one control point less to define the spline.

If we have more segments, then we run into a small problem. The next segment would want to calculate the new value for the point $q_2$, but we need that for calculating $q_1$. This can be solved, if we take thirds along the line between consecutive tips.

So all we need to do for the $C^2$ smooth Bezier spline would be to specify tips instead of control points and two of the first and two of the last control points. In our current example:

• For the first and last segment, take $p_2$ to be exactly in the middle of $p_1$ and $Tip_1$; take $r_1$ to be in the middle of $r_2$ and $Tip_2$.
• For the middle segments, divide the segment $[Tip_1, Tip_2]$ into 3 parts, after the first third comes $q_1$ and after the second third comes $q_2$.

When this is done, find the correct positions for the $C^1$ smoothness points. In our example, take $p_3$ to be in the middle of $p_2$ and $q_1$. Take $q_3$ to be in the middle of $q_2$ and $r_1$.

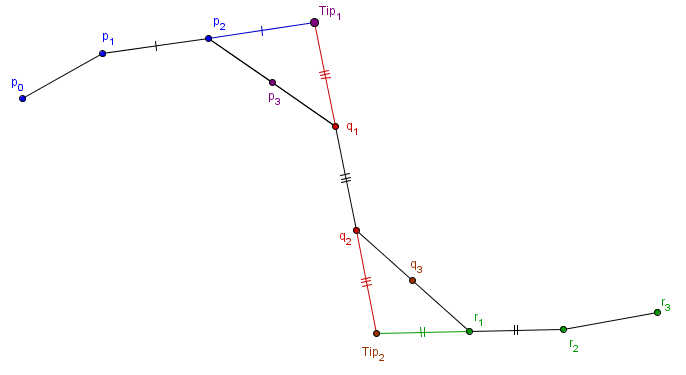
These are the $C^2$ smooth joints in the Stärk's construction. You read more about it here:
https://www.rose-hulman.edu/~finn/CCLI/Notes/day18.pdf

Finally you should also have $C^2$ smooth Bezier splines that may look like:

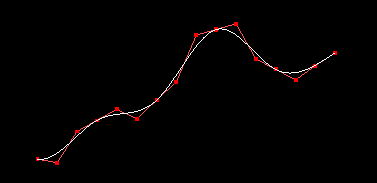
The first one is the same that was shown in the previous article as an example. 

Task is to create both $C^1$ and $C^2$ smooth Bezier splines. The first images shown here are from a fixed set of control points. The second images are using randomly generated control points.

The solution should allow user to switch between the test set and random set. Also switch between $C^1$ and $C^2$ smoothness.

In the material it was also mentioned, that if you transform the control points with an affine transformation, then the resulting curve is also correctly transformed. Ie the curve is affine invariant. In order to try this out, also rotate the control points around the y-axis, see if the curve behaves as expected.

JavaScript

Three.js provides us with a class that creates a cubic Bezier curve. We will use that class to create our segments, after we have found the correct control point values for a given smoothness.

Base code is located at:
https://cglearn.codelight.eu/files/course/11/BezierSplineJS.zip

C++

In C++ I ported the Three.js cubic Bezier curve functions, because there did not seem to be easily available implementations of it. Because we are at a lower level here, in C++ part of the task is updating the data sent to the VBO-s of the spline. Otherwise the task is similar, we use the cubic Bezier curves to draw a spline, but manipulate the control points so that the spline is $C^1$ and $C^2$ smooth.

Base code is located at:
http://cglearn.codelight.eu/files/course/11/BezierSplineCPP.zip